Wir kennen ja aus unserem Alltag durchaus das Prinzip von Parkettierungen, also von Fl├żchenf├╝llungen mit Hilfe regelm├ż├¤iger Formen. Normalerweise sind diese Parkettierungen regelm├ż├¤ig und periodisch, angefangen von schlichten, platonischen Parkettierungen wie Schachbrettern und Honigwaben ├╝ber archimedische und (lediglich) homogene bis hin zu inhomogenen Parkettierungen. Eine sch├Čne Archimedische Parkettierung ist (meiner Meinung nach) diese hier:

Diese Parkettierungen unterliegen allerdings gewissen Einschr├żnkungen hinsichtlich ihrer Symmetrie - sie k├Čnnen lediglich eine ein-, zwei-, drei-, vier- oder sechsz├żhlige Symmetrie haben, also Symmetrien in Winkeln von 360┬░, 180┬░, 120┬░, 90┬░ oder 60┬░, aber beispielsweise keine f├╝nfz├żhlige Symmetrie mit einem Winkel von 72┬░ oder gar h├Čherz├żhlige Symmetrien.
Neben den regelm├ż├¤igen periodischen Parkettierungen gibt es aber auch noch regelm├ż├¤ige, jedoch aperiodische Parkettierungen. Um solche Parkettierungen handelt es sich bei der "Familie" der Penrose-Parkettierungen:

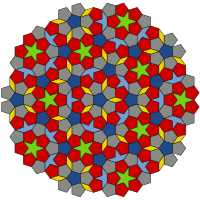
Wie man sieht, weisen die Penrose-Parkettierungen 2 interessante Merkmale auf:
- Sie sind, wie erw├żhnt, aperiodisch, d.h. das Muster, das auf ihnen entsteht, wiederholt sich trotz der Regelm├ż├¤igkeit nicht (wohl aber Teile des Musters) - man kann das Muster nicht mit einer identischen, aber verschobenen Kopie von sich selbst zur Deckung bringen wie bei den periodischen Mustern. Ja, das h├żtte ich vorher mal generell erkl├żren k├Čnnen, aber man sieht's nun mal da oben ganz nett.
- Sie haben - ei der Daus! - 'ne f├╝nfz├żhlige Symmetrie.
