Pentargoras

Das Pentagramm ist nicht erst in Mode, seit Satanismus, Okkultismus und Hexerei wieder chic sind. Es ist nicht nur ein Symbol für Böse oder Gut oder, wie bei uns Diskordianern, ein Symbol für Unordnung, es ist nicht nur ein beliebtes Symbol auf Staatsflaggen (Man denke an den roten Stern der alten Sowjetunion, den weißen Libertystar der Amerikaner, der auch gleich zigmal auf ihrer Fahne prangt oder an die 12 gelben Sterne Europas. Oder man schaue mal nach Marokko oder Äthiopien, da sind es wirklich Pentagrammata.) oder das Zeichen für irgendwelche fünfbeinigen Dämonen, die einen des Nachts heimsuchen, oder das Abzeichen der babylonischen Ärzte oder das sumerische Symbol für Erhabenheit, nein, es ist auch (Endlich, ihr habt sicher schon drauf gewartet, gell? Na, es wird ja auch Zeit!) das Abzeichen des alten Geheimbundes der Pythargoräer, welche wiederum die Gefolgsleute des anerisischen Erzengels Pythargoras waren. Und ausgerechnet dieses Zeichen war es, das ihr rationales Weltbild mit seinen rationalen Zahlen ins Wanken brachte und die Mathematik den ersten Schritt in Richtung Chaos machen ließ.

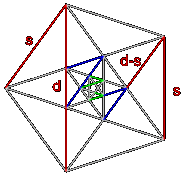
Die Pythargoräer glaubten nämlich, daß sich die ganze Welt sich durch ganze Zahlen und Verhältnisse derselben zueinander darstellen ließe. Eine ganze Weile lang funktionierte ihre Welt so auch wunderbar, bis einer von ihnen, Hippasos, auf die Idee kam, das Verhältnis der Länge s der Seiten des Fünfecks zur Länge d der Diagonalen (die ein Pentagramm formen) zu berechnen. Dabei stolperte er nicht nur über den goldenen Schnitt und die Fibonacci-Sequenz, sondern auch gleich über die Inkommensurabilität, das heißt die Teilerfremdheit, das heißt die Unvereinbarkeit der beiden Zahlen, das heißt ihr irrationales Verhältnis.

Dies sieht man anschaulich durch die geometrische Methode der Wechselwegnahme: Man gibt der Seite des Pentagons eine beliebige, ganzzahlige Länge. Stünden die beiden Zahlen in einem rationalen Verhältnis, so würde das Wegnehmen von s aus d irgendwann zum Wert 0 führen, stattdessen erhalten wir ein neues Pentagon mit einem neuen Pentagramm darin, mit demselben Verhältnis s:d, was bei erneuter Wechselwegnahme wieder zu einem Pentagon-Pentagramm-Paar führt, mit demselben Verhältnis s:d, bis man schließlich (der Fibonnacci-Sequenz folgend) bei der kleinstmöglichen Ganzzahl, 1, landet. Man kann den Anfangswert für die Seitenlänge des ersten Pentagons beliebig wählen, man landet am Ende immer bei 1. Das heißt, es gibt kein einfaches, rationales Verhältnis s:d, das Verhältnis lässt sich nicht als Bruch ganzer Zahlen ausdrücken und ist somit irrational.

Für die Pythargoräer war dies quasi der Todesstoß, sie gingen ein oder entwickelten sich weiter. Ihr rationales Weltbild war zerbrochen, die Welt hatte an Ordnung verloren, ein Prozess, der nicht aufzuhalten war. Übrigens deutet die Grafik schon einen erst kürzlich vollzogenen Schritt an: Die Wiederholung der verschachtelten Pentagon-Pentagramm-Paare erinnert entfernt an die Selbstähnlichkeit der Fraktale…

Und wo wir gerade bei Geheimbünden sind: Wer findet den in der Grafik versteckten Hinweis auf die Freimauerer?