Spontane Selbstentzündung durch aufgestaute Gedankenfürze

[fehlgeleitet]

Ich bin fast geneigt, Žižeks Credo umzukehren: Das Durchschreiten des Christentums führt nur insofern zu Atheismus und Materialismus, als man beim Durchschreiten merkt, dass das Christentum eine Sackgasse ist, und sich ergo entscheidet, einen anderen Weg einzuschlagen.

Hat nur indirekt was mit dem Thema zu tun, aber vielleicht kann man allgemein sagen, dass der Wert der negativen Erkenntiss begrenzt ist?

Der Stalker zb durchläuft nach einer Theorie 4 Phasen.

Romantisierung - Desillusion - narzistische Raserei - Reue - und das ganze geht wieder von vorne los. Es gibt Fälle von Stalking die bis zu 50 Jahre angedauert haben sollen. Insofern scheint die Desillusionierungsphase herzlich wenig gebracht zu haben

[Tarvoc]

Insofern scheint die Desillusionierungsphase herzlich wenig gebracht zu haben

Jupp, dementsprechend kann man sich den ganzen Quark mit dem "Durchschreiten" des Christentums womöglich auch gut sparen.

[fehlgeleitet]

Insofern scheint die Desillusionierungsphase herzlich wenig gebracht zu haben

Jupp, dementsprechend kann man sich den ganzen Quark mit dem "Durchschreiten" des Christentums womöglich auch gut sparen.

ich frag mich grad wie man Stalker und andere die in so einer Schleife festhängen dann therapieren könnte? Wäre es vielleicht ein Therapieerfolg wenn man die Emotionskette invertieren könnte, also Reue - narzistische Raserei - Desillusion - Romantisierung?

Der normale Fall ist ja, dass Herr A glaubt eine Beziehung mit Frau B zu führen (Romantisierung). Dann spricht er Frau B an, die dann die Polizei holt, weil sie Herrn A verboten hat sich ihr zu näheren (Desillusion), dann schmiedet Herr A Rachepläne und stellt alle ihre persönlichen Daten ins Netz (narzistische Raserei), um sich dann später wieder selber bei der Polizei anzuzeigen, um seine imaginäre Beziehung zu Frau B wiederherzustellen (Reue).

Invertieren wir den kreislauf, könnte das dabei rauskommen:

Herr A könnte sich also stattdessen Verbrechen beschuldigen die er gar nicht begangen hat, zum Beispiel behaupten er sei Mitglied einer Terrororganistation (Reue), sobald er deswegen festgesetzt wird einen Wutanfall kriegen und um sich schlagen (narzistische Raserei), danach in der Psychatrie feststellen, dass man ihn nicht ernst nimmt (Desillusion) und mit Hilfe ein paar gute-laune-pillen an ein happy-end glauben (romantisierung).

shit, das haut auch nicht an, offenbar. Einen vernünftigen Therapievorschlag habe ich leider nicht.

[Cpt. Bucky Saia]

Man könnte auch einfach ein kantholz nehmen

[fehlgeleitet]

Man könnte auch einfach ein kantholz nehmen

in den 50 jahre laufenden fällen ist eine solche maßnahme vermutlich dem bedürfniss der betroffenden entsprechend.

alles gute nachträglich übrigens.

[Tarvoc]

ich frag mich grad wie man Stalker und andere die in so einer Schleife festhängen dann therapieren könnte?

Wie waren wir noch gleich auf das Thema Stalking gekommen?

[fehlgeleitet]

ich frag mich grad wie man Stalker und andere die in so einer Schleife festhängen dann therapieren könnte?

Wie waren wir noch gleich auf das Thema Stalking gekommen?

oder anders gefragt: wie kann man christen und sonstwie religiöse therapieren? die suche nach dem grund wie sie irgendwann mal dahin gekommen sind dürfte sich als schwierig erweisen...

edit: also wenn falsifikation als mainerkenntnisstool nicht mehr ausreicht, was dann

[fehlgeleitet]

Vielleicht hat das was mit dem vorherigen zu tun - mein liebligssatz aus einem scifi-film.

"Sie wissen nicht was sie tun, sie denken sie befinden sich in einer Simulation."

Irgendwie denke ich dieser Satz trifft auf viele meiner Zeitgenossen zu

Vielleicht ist es nicht möglich die Realität vollständig zu virtualisieren, und es wird immer das dumpfe gefühl zurückbleiben sich in einer art blase zu befinden. virtuell heißt ja auch "fast". Vielleicht ist auch der Ansatz falsch, dass Gehirn als eine Art Schaltkreis zu sehen, von dem es ausreichen würde die input-schnittstelle zu bedienen. dementsprechend würde persönliche entwicklung etwas anderes bedeuten als ein paar innerpsychische prozesse in gang zu setzen.

sie würde nämlich dann vor allen dingen auch in der außenwelt stattfinden.

[fehlgeleitet]

Bei der Integration von Flüchtlingen und Immigranten in die westliche Gesellschaft fällt mir auf, dass man eine immense Ausbildung braucht (und Geld im Rücken) um tatsächlich Teil der westlichen Gesellschaft zu sein.

Die kann natürlich niemand vorweisen, der aus einer krisengebeutelten Region kommt und wird sie auch niemals bekommen, wenn er schon mitten im Leben steht. Und so bleibt am Ende nur die Koranschule oder eine Karriere als Gangster. Hinzu kommt die permanente Bedrohung durch abschiebung, so dass sich die Mühe kaum lohnt sich was aufzubauen, was im nächsten Moment wie ein Kartenhäuschen zusammenfallen könnte.

Vielleicht ist Demokratie am Ende zu vorrausetzungsreich, als das sie realpolitisch funktionieren kann. Vielleicht wählen Menschen auch die Rechtspopulisten, weil sie mit dem politischen Diskurs überfordert sind.

Wo die wissenschaften zu arrogant sind, können Religiöse und ähnliche weiterhin punkten.

[fehlgeleitet]

apropro vorraussetzungen:
hier eine hübsche mathematische Spielerei, die vermutlich der Realität sehr nahe kommt.

Politische Parteien scheinen sich immer weiter anzunähern. Ein Grund sind spieltheoretische Überlegungen, so dass wenn man versucht die maximale Anzahl von Stimmen zu kriegen man versucht der Meinung der meisten zu entsprechen.

Es gibt aber noch weitere Gründe, intressantere behaupte ich. In der linearen Optimierung lassen sich Probleme der gestalt das "Minimiere x, unter der Bedingung das y>0 ist" in "Maximiere y, unter der Bedinung das x<0 ist" umformulieren und haben erstaunlicherweise immer dieselbe lösung

Wenn ich also sage: "Ich möchte die Wettbewerbsfähigkeit Deutschlands erhöhen, ohne dabei zuviel soziale Ungleichheit zu schaffen." ist das die gleiche Aussage wie "Ich möchte die soziale Ungleichheit verringern, ohne dass dabei die Wettbewerbsfähigkeit Deutschlands zu sehr leidet."

Denn mathematisch handelt es sich hier um ein Minimax-problem bei denen es darum geht einen bestimmten Zustand zu optimieren ohne dabei eine Nebenbedingung zu verletzen. Nun kann man aber wie oben gesagt beweisen, dass beide Aussagen die gleiche Lösungen haben, vorrausgesetzt es handelt sich um lineare gleichungen und wir gehen in beiden aussagen von gleichen definitionen der sozialen ungleichheit bzw. wettbewerbsfähigkeit aus.

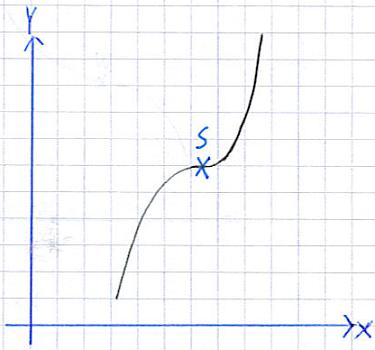
Man kann sich das so vorstellen, dass ich in jedem Fall bei dem Sattelpunkt einer Funktion lande, egal ob ich nun von links oder von rechts komme: